誕生日が一致する確率
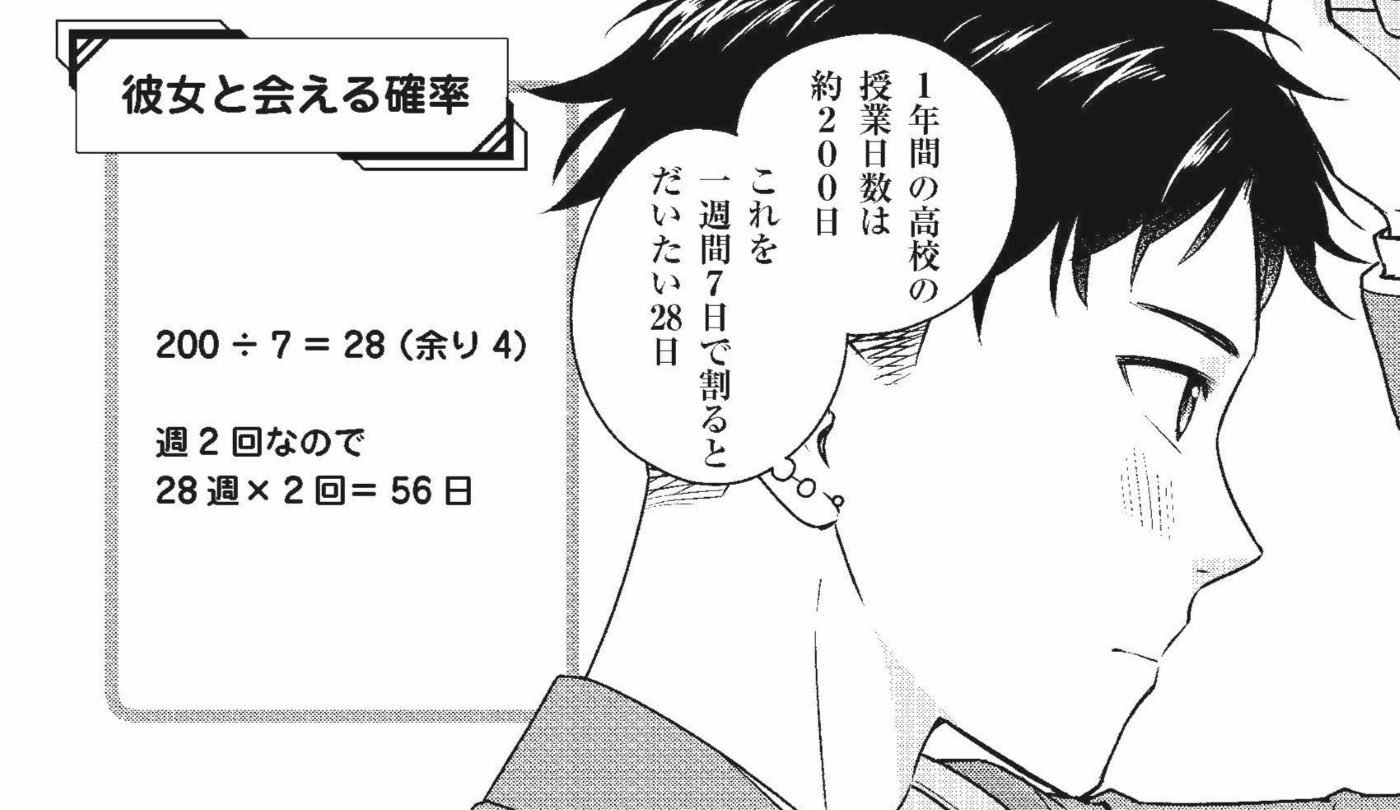
2人の誕生日が同じになる確率
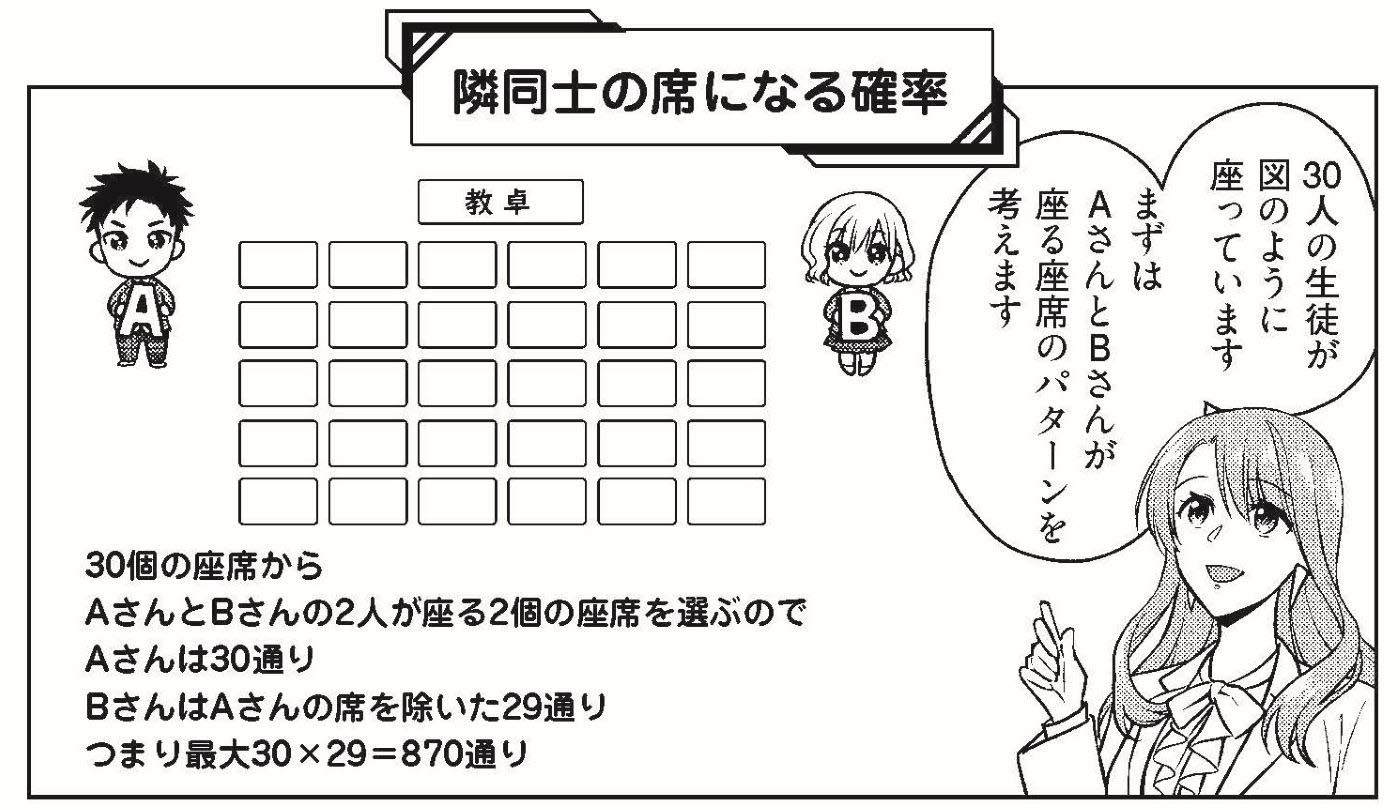
参加している読書サークル23人のなかで、誕生日(何月何日)が同じ人がいるのを発見して運命的なものを感じました。はたして、23人のなかで誕生日が一致する人がいる確率はどの程度なのでしょうか?
ある集団のなかで誕生日が同じ人が少なくとも1組以上いる確率を求めるには、23人の誕生日がすべて異なる確率を求め、それを1から引きます。
まず、23人のうち最初の1人は、365日のうちのどの誕生日でもよいので、これを確率で表すと365分の365で1です。
2人目は1人目と異なる誕生日なので、365日から1人目の誕生日を引いた364日のうちのどれかになります。確率で表すと365分の364です。この2人の誕生日が異なる確率は、1×364/365=364/365。逆にいうと、誕生日が同じである確率は1-364/365=1/365 です。
23人のなかで誕生日が同じ人のいる確率は?
3人目は363日のどれかになればよいので、確率は363/365ですそして3人の誕生日がすべて異なる確率は、1×364/365×363/365と計算します。
こうして計算を続けていく、23人すべての誕生日が異なる確率は次のようになります。
1×364/365×363/365×…×343/365=約0.49=49%
つまり、23人のなかに少なくとも1組以上、誕生日の一致する人がいる確率は1-0.49=0.51=51%です。23人いれば、約51%の確率で誕生日の一致する人がいるのですから、それほど珍しいことではありませんね。
出典:『マンガでわかる 図解 眠れなくなるほど面白い 確率の話』
【書誌情報】
『マンガでわかる 眠れなくなるほど面白い 図解 確率の話』
著者:野口哲典(マンガ:田伊りょうき)
当社の「眠れなくなるほど面白い 図解」シリーズをよりわかりやすく解説する「マンガ図解」シリーズの第1弾! 我々の日常に深く入り込んでいる「確率」。朝の天気予報で「降水確率」を確認したり、野球シーズンには勝率や打率をチェックしたりする方もいると思います。ジャンケンやサイコロの目、ゲームのガチャやくじなどの当たる確率、人生の節目にあたる受験の合格確率やプロポーズの成功確率など、実にさまざまなシーンで「確率」の話になるのです。そんな「確率」をマンガと図で解説し、面白く読み進めながら知識を得られる一冊。「運命の出会い」を確率にするとどのくらいになるのか、最低でも一校は合格するための受験の仕方など、勉強としてではなく実際に役立つ確率の話ばかりなので、ぜひご一読ください。
公開日:2024.06.26