あこがれの人と隣どうしになりたい！
好きな人が隣にくる確率は意外に高い？
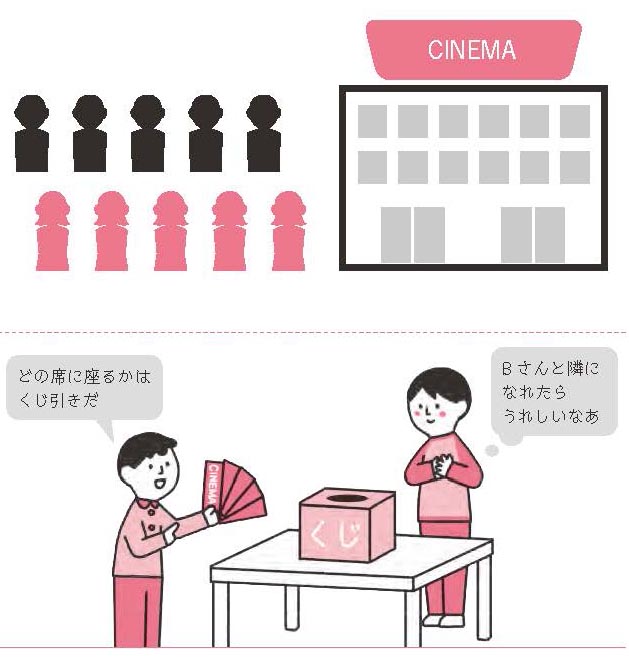
サークル仲間、男女５人ずつの10人で映画を観に行くことになりました。10人が横一列に並ぶように座席指定券を購入し、どの席へ座るかは、くじで決めることにしました。
さて、このときＡくんが密かにあこがれているＢさんと隣どうしになれる確率は、どのくらいあるでしょうか？
２人で１人と考える
まず、10人が横一列に並んで座る順列を考えます。
10! ＝10×９×８×７×６×５×４×３×２×１＝362万8,800通り
このなかでＡくんとＢさんの２人が隣どうしになる場合の数が何通りあるかがわかれば、確率を求めることができます。
この場合、すでにこの２人が隣どうしになっていると考えましょう。そして、ほかの８人との並び順がどうなるかを求めます。要するに、この２人を１人と見なし、９人の順列を考えるわけです。
９!＝９×８×７×６×５×４×３×２×１＝36万2,880通り
ただし、この２人の順番は逆になってもいいので、実際にはこの２倍の並び方があります。したがって、この２人が隣合う場合の数は36万2,880 通りの２倍、72万5,760通りです。
つまり、10人が横一列で座席に座るとき、２人が隣どうしになる確率は、72万5,760÷362万8,800＝1/5
５分の１と意外に高い確率で隣どうしになれるのです。
出典：『マンガでわかる 図解 眠れなくなるほど面白い 確率の話』
【書誌情報】
『マンガでわかる 眠れなくなるほど面白い 図解 確率の話』
著者：野口哲典（マンガ：田伊りょうき）
当社の「眠れなくなるほど面白い 図解」シリーズをよりわかりやすく解説する「マンガ図解」シリーズの第１弾！ 我々の日常に深く入り込んでいる「確率」。朝の天気予報で「降水確率」を確認したり、野球シーズンには勝率や打率をチェックしたりする方もいると思います。ジャンケンやサイコロの目、ゲームのガチャやくじなどの当たる確率、人生の節目にあたる受験の合格確率やプロポーズの成功確率など、実にさまざまなシーンで「確率」の話になるのです。そんな「確率」をマンガと図で解説し、面白く読み進めながら知識を得られる一冊。「運命の出会い」を確率にするとどのくらいになるのか、最低でも一校は合格するための受験の仕方など、勉強としてではなく実際に役立つ確率の話ばかりなので、ぜひご一読ください。
公開日：2024.06.24
- この記事を共有する！
オススメ記事
