ライブの曲順決めは何パターン?計算の決め手は「階乗」【マンガでわかる 図解 眠れなくなるほど面白い 確率の話】


演奏会での順番を決めるには?
3人の演奏順は何通り?
3人の奏者によるピアノの演奏会があります。このとき、3人が演奏する順番は全部で何通りあるでしょう?
3人の演奏者をそれぞれA、B、Cとすると、「ABC」「ACB」「BAC」「BCA」「CAB」「CBA」の6通りあります。下の図のような樹形図にするとわかりやすいです。
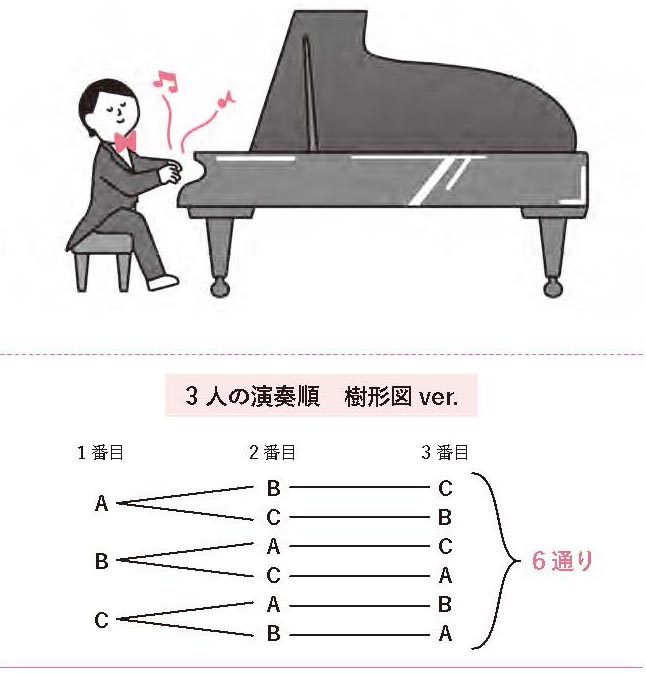
階乗で求めてみよう
このように、樹形図でもれなく数えることもできますが、もっと簡単に計算で求める方法を考えてみましょう。
A、B、Cの3人の場合、最初に演奏するのは、3人のうちの誰でもよいので3通りです。次に演奏するのは、最初に演奏した人以外の2人のうちのどちらかなので2通りになります。最後に演奏するのは、残った1人だけなので1通りしかありません。
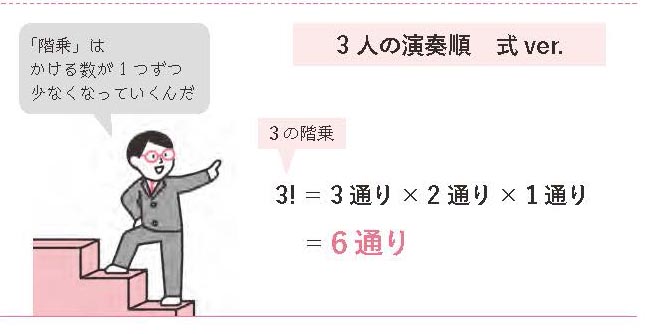
したがって、次のかけ算で3人が順番に演奏する場合の数を求めることができます。
3通り×2通り×1通り=6通り
このかけ算は、階段を下っていくように、1ずつ少ない数をかけ合わせていくことから「階乗」と呼ばれています。そして、階乗は数字のうしろに「!」マークをつけて表します。異なるn個のものを順番に並べるときの並べ方は「n!」通りと表記されるのです。
たとえば演奏者が5人なら、その演奏順は5!=5×4×3×2×1=120通りです。
出典:『マンガでわかる 図解 眠れなくなるほど面白い 確率の話』
【書誌情報】
『マンガでわかる 眠れなくなるほど面白い 図解 確率の話』
著者:野口哲典(マンガ:田伊りょうき)
当社の「眠れなくなるほど面白い 図解」シリーズをよりわかりやすく解説する「マンガ図解」シリーズの第1弾! 我々の日常に深く入り込んでいる「確率」。朝の天気予報で「降水確率」を確認したり、野球シーズンには勝率や打率をチェックしたりする方もいると思います。ジャンケンやサイコロの目、ゲームのガチャやくじなどの当たる確率、人生の節目にあたる受験の合格確率やプロポーズの成功確率など、実にさまざまなシーンで「確率」の話になるのです。そんな「確率」をマンガと図で解説し、面白く読み進めながら知識を得られる一冊。「運命の出会い」を確率にするとどのくらいになるのか、最低でも一校は合格するための受験の仕方など、勉強としてではなく実際に役立つ確率の話ばかりなので、ぜひご一読ください。
この記事のCategory
オススメ記事

人はそれを奇跡と呼ぶ!理想の恋人に出会う確率は?【マンガでわかる 図解 眠れなくなるほど面白い 確率の話】
コインを投げて表と裏が交互に出るのはたったの6.25%!表か裏が連続で3回以上出る確率とは!?【マンガでわかる 図解 眠れなくなるほど面白い 確率の話】

徹底検証!「残りものには福がある」はホント?くじを引く順番と確率【マンガでわかる 図解 眠れなくなるほど面白い 確率の話】

絶対に外したくないテスト範囲の予想で取り入れるべき一番賢い方法とは!?【マンガでわかる 図解 眠れなくなるほど面白い 確率の話】

最初の決断を変えると当せん確率UPする理由とは!?【マンガでわかる 図解 眠れなくなるほど面白い 確率の話】

確率1/10のくじは10回引けば当たるのか?知れば得するくじの秘密【マンガでわかる 図解 眠れなくなるほど面白い 確率の話】
無謀な挑戦!?ジャンボ宝くじを10枚買った時の1等が当たる確率とは!?【マンガでわかる 図解 眠れなくなるほど面白い 確率の話】





