知っていると人生が好転するチャンスを掴める確率の求め方とは!?【マンガでわかる 図解 眠れなくなるほど面白い 確率の話】


確率の求め方
事象の起き方の合計数が「場合の数」
確率を求めるためには、確率の公式に当てはめる分母と分子の数を明らかにします。そのために必要な知識が、「場合の数」と呼ばれるものです。
場合の数とは、ある出来事の結果にどのような場合があるかを重複なく数え上げた、事象の起き方の合計数のことです。
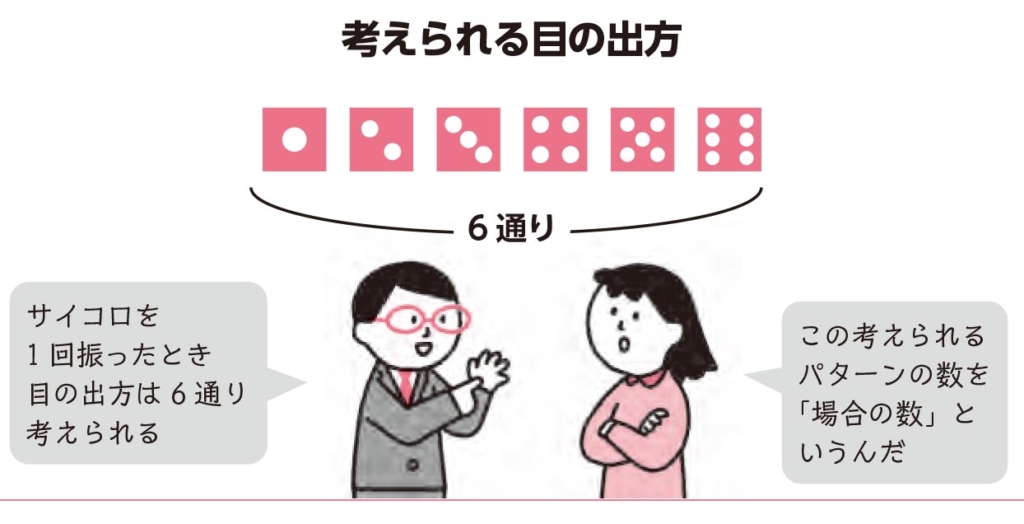
たとえば、1つのサイコロを振ったときに出る目は全部で6通りあります。この6通りの目の出方が場合の数です。
このことから、3の目が出る確率は6分の1になります。
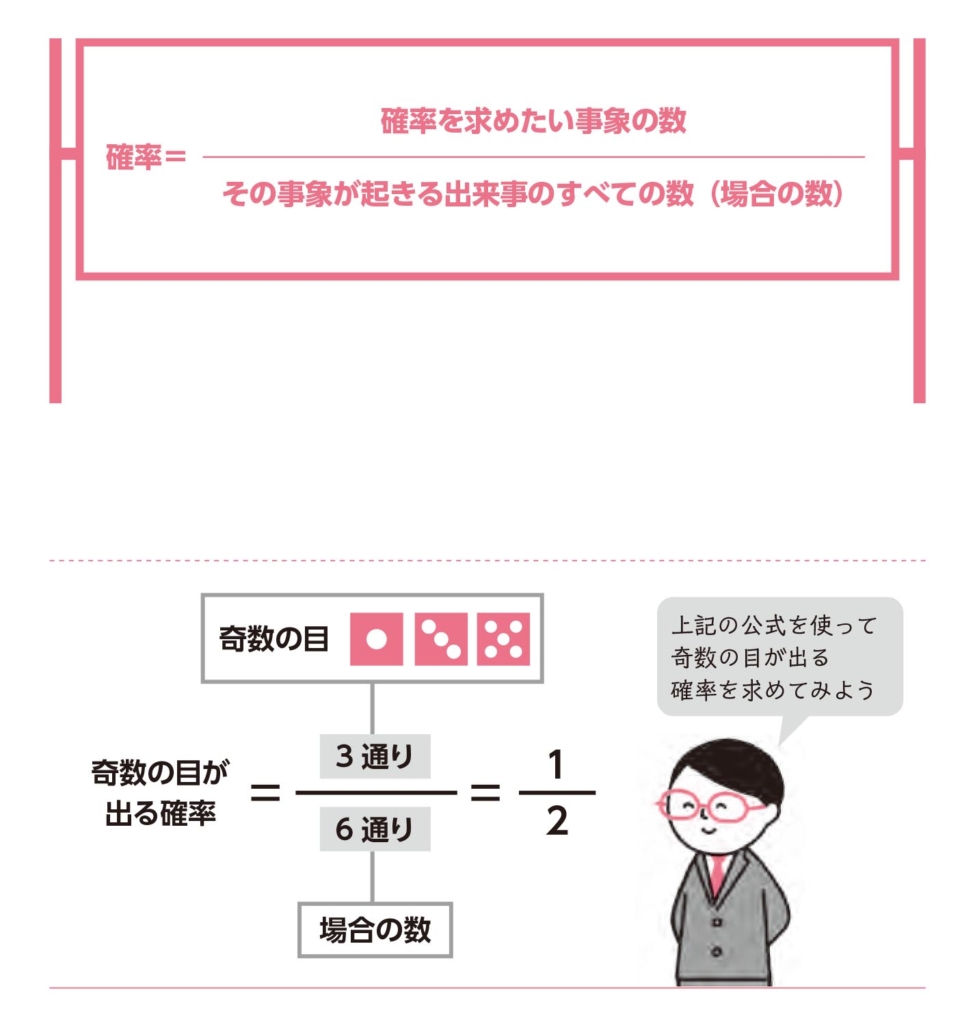
また、1つのサイコロを振って奇数の目が出る確率ならば、奇数の目は1、3、5の3通りなので、確率は6分の3、つまり2分の1になるというわけです。
「場合の数」で確率がわかる
このように、場合の数は数学的確率を求めるときに必要不可欠な数字です。そして、場合の数さえわかれば、すぐに確率を求めることができます。
数学的確率は、次の公式で求められます
出典:『マンガでわかる 図解 眠れなくなるほど面白い 確率の話』
【書誌情報】
『マンガでわかる 眠れなくなるほど面白い 図解 確率の話』
著者:野口哲典(マンガ:田伊りょうき)
当社の「眠れなくなるほど面白い 図解」シリーズをよりわかりやすく解説する「マンガ図解」シリーズの第1弾! 我々の日常に深く入り込んでいる「確率」。朝の天気予報で「降水確率」を確認したり、野球シーズンには勝率や打率をチェックしたりする方もいると思います。ジャンケンやサイコロの目、ゲームのガチャやくじなどの当たる確率、人生の節目にあたる受験の合格確率やプロポーズの成功確率など、実にさまざまなシーンで「確率」の話になるのです。そんな「確率」をマンガと図で解説し、面白く読み進めながら知識を得られる一冊。「運命の出会い」を確率にするとどのくらいになるのか、最低でも一校は合格するための受験の仕方など、勉強としてではなく実際に役立つ確率の話ばかりなので、ぜひご一読ください。
この記事のCategory
オススメ記事

「コイン投げと野球の打率では種類が違う?」数学的確率と統計的確率とは!?【マンガでわかる 図解 眠れなくなるほど面白い 確率の話】

知っていると人生が好転するチャンスを掴める確率の求め方とは!?【マンガでわかる 図解 眠れなくなるほど面白い 確率の話】
無謀な挑戦!?ジャンボ宝くじを10枚買った時の1等が当たる確率とは!?【マンガでわかる 図解 眠れなくなるほど面白い 確率の話】

「必ず当たる」は正義!得をすることよりも確実に当たる方に魅力を感じるのはなぜ?【ゼロからわかる知らないと損する行動経済学】

「本日限り!」と期間を制限されるとつい購入してしまうのはなぜ?意識をしていなくても影響を与えている身近な損失回避性とは!?【ゼロからわかる知らないと損する行動経済学】

『プロサッカークラブをつくろう! ロード・トゥ・ワールド』 スペイン強豪クラブのレジェンド「ロナウジーニョ」「ガイスカ・メンディエタ」や、現役スター選手が多数登場!

「自律神経失調症」と「うつ病」の違いとは?【図解 ストレスの話】
求人情報
美容クリニックの予約管理・お問い合せ対応/未経験OK/賞与年3回/医療脱毛社割有/勧誘ナシ/残業少なめ
セブンエー美容株式会社
勤務地:福岡県 福岡市雇用形態:正社員給与:月給22万円~スポンサー:求人ボックス
インテリア家具の品質管理/ブランド品質を支える、専門性を活かせるポジション
株式会社ミサワ
勤務地:東京都雇用形態:正社員給与:月給27万円~35万円スポンサー:求人ボックス
残業なし&直行直帰!前職以上の給与を約束&賞与100万円超の実績!新築の建築施工管理スタッフ
株式会社中山建設
勤務地:愛知県雇用形態:正社員給与:月給40万円~57万円スポンサー:求人ボックス
重度障がい者グループホームの生活サポートスタッフ/未経験歓迎!6時ー9時×週1日の単発シフトもOK
特定非営利活動法人大地
勤務地:東京都雇用形態:アルバイト・パート給与:時給1,250円~スポンサー:求人ボックス
タクシーの養成乗務員
立川観光自動車株式会社
勤務地:東京都雇用形態:正社員給与:月給20万9,652円~41万4,950円スポンサー:求人ボックス
タクシードライバー/入社祝い金15万円支給/未経験歓迎
イースタンモータース東京株式会社
勤務地:東京都雇用形態:正社員給与:月給35万円~70万円スポンサー:求人ボックス




