雑学

日本酒の魅力を引き出す美しき二杯、瀬戸の花嫁と黄昏【THE カクテルバイブル500】
ビール&日本酒など【瀬戸の花嫁(Setonohanayome)】 白無垢姿の花嫁の秘めた思いを表現 白無垢姿の美しい花嫁の姿をイメージした、日本酒ベースのカクテル。中に沈めたチェリーは花嫁の秘めた思いを表現。ライチやゆず […]

火山の噴火の仕組みはプロ野球の優勝祝勝会のビール掛けと同じ?驚くべき噴火の話!【眠れなくなるほど面白い 図解 地学の話】
火山噴火はどんなしくみで起きるのか? 素朴な疑問です。どうして火山は噴火するのでしょうか? 身近なものでも不思議があります。例えば、プロ野球の優勝祝勝会などで、選手がビールをよく振ってから一気に栓せんを抜くと、泡立ったビ […]

ずっと浮かび続ける鳥! カモの撥水加工技術とは!?【眠れなくなるほど面白い 図解 鳥の話】
カモは自分の脂を羽毛に塗って撥水加工している 防水ボディのヒミツ 池や川で気持ちよさそうに浮かんでいるカモたち。その体が水に沈まないのは、足でこぐ力や羽の形のおかげだけではありません。実はもう1つ、大きなヒミツがあります […]

イギリスのパブが発祥といわれている甘くて爽快なビールカクテルとは!?【THE カクテルバイブル500】
ビール&日本酒など【サムライロック(Samurai Rock)】 日本酒とライムだけのシンプルなレシピ 日本酒にライムで風味づけしただけの、材料も手順もいたってシンプルなカクテル。コーディアルライムジュースの甘さが日本酒 […]

約4割が浮気で生まれた子!? 見た目と実情は違う「おしどり夫婦」由来のオシドリの生態【眠れなくなるほど面白い 図解 鳥の話】
「おしどり夫婦」の由来であるオシドリは普通に浮気する 名前とは異なる実態 仲の良い夫婦のことを表す「おしどり夫婦」という言葉は、オシドリに由来するといわれています。色鮮やかな羽を持つオスと、落ち着いた色合いのメスが川や湖 […]

沖縄の夏を一杯に!ゴーヤと泡盛で作る琉球カクテルとは?【THE カクテルバイブル500】
ビール&日本酒など【ゴーヤ琉球カクテル(Goya Ryukyu Cocktail)】 うちなーんちゅ御用達のカクテル 地元、沖縄の人々に愛されている定番のフローズンカクテル。沖縄が世界に誇る銘酒、泡盛と、県の特産品ゴーヤ […]
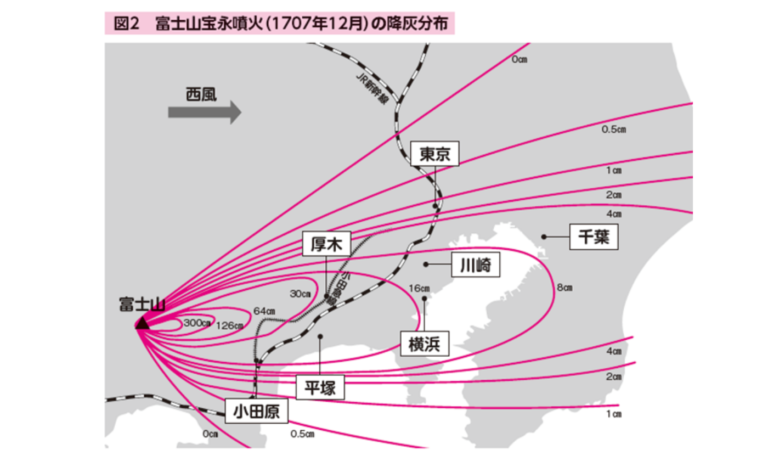
近いうちに富士山が噴火する可能性はあるのか?首都圏が大災害になるその日とは!【眠れなくなるほど面白い 図解 地学の話】
宝永噴火に匹敵する噴火があれば首都圏は大災害 富士山はいつ噴火しますか?これはよくある質問です。ですが、正確に答えるのは非常に難しいのです。まず、火山の噴火を予測する方法には、短期的な直前予測と長期的な予測があることを知 […]

「水辺の宝石 カワセミ」は指輪の代わりに”魚”で求婚する!?【眠れなくなるほど面白い 図解 鳥の話】
カワセミは捕った魚をメスに渡してプロポーズする 愛を運ぶ青い鳥 鮮やかな青い羽が目を引く「カワセミ」は、川や池の近くにすむ小さな鳥です。その美しい姿から「水辺の宝石」とも呼ばれています。 春になると、カワセミのオスは少し […]

日本酒・焼酎好き必見!和のスピリッツで楽しむカクテル【THE カクテルバイブル500】
ビール&日本酒など【カイピリーニャ(Caipirinha)】 ブラジルのお酒を使った爽やかな一杯 カクテル名は「田舎のお嬢さん」から。ベースに使用するカシャッサ(ピンガ)は、サトウキビを使ったブラジルのお酒。ライムと砂糖 […]
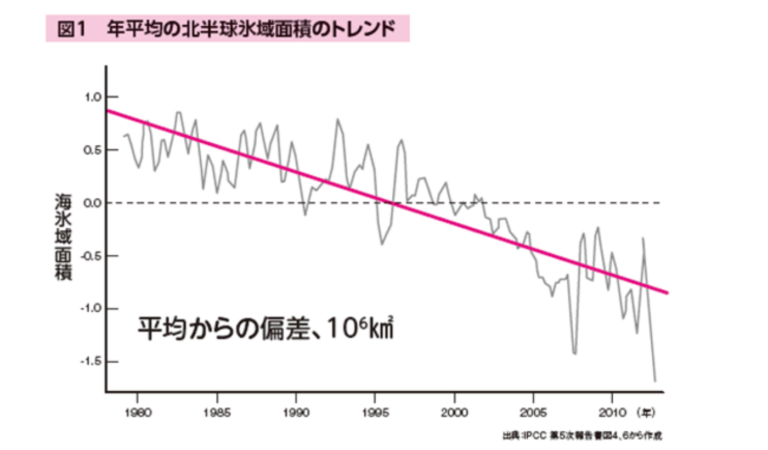
地球規模の大きな危機!温暖化で北極の氷が溶けるとどうなってしまうの?【眠れなくなるほど面白い 図解 地学の話】
温暖化熱を海水が吸収して膨張し、海面が上昇 地球温暖化に伴い、海面上昇することが懸念されています。IPCC(気候変動に関する政府間パネル)では数年おきに世界中の科学者が集まって、科学的な知見を集めた報告書を提出しています […]

世界の最低気温は-89.2度!? 北極と南極では”南極の方が寒い”ワケ【眠れなくなるほど面白い 図解 地学の話】
陸地か否か、二つの極圏で異なる条件 世界での最低気温の記録は南極のロシアのボストーク基地(図1)で1983年7月に記録されたマイナス89.2℃です(2008年8月10日、衛星データの分析により、南極大陸東部の高地でマイナ […]

雪山で眠くなる原理と同じ!? 入浴で自然に入眠できるワケ【1週間で勝手にぐっすり眠れる体になるすごい方法】
人間は体温が下がるときに眠くなる 夜、だんだん眠くなるとき、私たちの体にはどんな変化があるのでしょうか。まず、リラックスして副交感神経が高まり、血管が拡張して心拍数や血圧、そして体温も下がります。眠りに最も重要なのが、こ […]
