改めて円について考えてみよう
●スウィングの再現性を実現する
Sスウィングの本論に入るまでに、もう少し基礎的な数学（幾何）の話にお付き合いください。
皆さんが「円」について最初に学ぶのは小学校３年生の頃です。当時の記憶をたどってみましょう。円の
定義は次のように書かれています。
「コンパスで描いたような丸い形を円という。円の真ん中の点を円の中心、中心から円のまわりまで引いた直線を円の半径という」
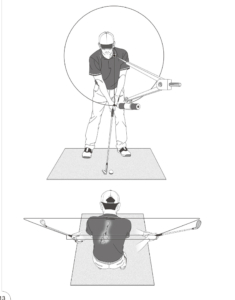
そこで改めて円について考えてみます。下のイラストをご覧ください。コンパスを使って円を描いている図です。
言うまでもなく、「円は、その中心である支点が動かず、半径の長さが一定なら、つねに同じ円を描く」ことがわかると思います。いつでも、どこでも、何度やっても、です。
これはスウィングで言うところの「再現性」に繋がります。いつでも、どこでも、１球目から、きちんとボールに当てられる……。スウィングの中心が動かず、スウィング中の腕とシャフトで作る半径の長さが一定なら、ダフリやトップは起きません。Sスウィングはこの原理を採用しています。
詳しくは、このあとおいおい明らかにしていきます。
円については、もう１つ確認しておきます。
それは「円を真上から見ると直線である」ということです（下イラスト）。ゴルフスウィングに応用して説明すると、直線だから方向性をだしやすいということです。先日、紹介した「よい選手はＸ点がタテに?れている」は「タテ
に振れているから、方向性のいいショットが打てるのだ」と理解してください。
出典：『ゴルフスウィングの真実 ジャストミートを確約するＳスウィング』著/佐久間馨
【書誌情報】
『ゴルフスウィングの真実 ジャストミートを確約するＳスウィング』
著者：佐久間馨
タイガー・ウッズ、ジャック・ニクラウスなど、プロゴルファーの名選手には共通したクラブの動きがある。その動き分析し、本書の著者が体系づけたスウィングが「Sスウィング」。 本書の構成は「Sスウィングのメカニズム」と「漫画でわかるＳスウィングの正体」の２部構成。 第１部では「クラブの動きと体の動き」の視点から、合理的なクラブの振り方を詳細なイラストとわかりやすいテキストを使って解説。アドレスからフィニッシュまでの動きについて、著者独自の理論を展開している。なかでも、「スライド・ダウン」、「ターンアップ」など従来のゴルフ用語にはない、スウィングの動きを表す言葉の解釈は一読の価値あり。 さらに、第２部「漫画でわかるＳスウィングの正体」は、ゴルフビギナーがSスウィングを学び、身に付けていくプロセスをストーリー漫画でわかりやすく紹介している。
公開日：2021.12.06
- この記事を共有する！
オススメ記事
