男女2人ずつ代表を選ぶ方法
男2人に女2人が対応する
男5人、女4人の計9人のなかから、男女それぞれ2人ずつ計４人の代表を選ぶとき、何通りの組み合わせがあるでしょうか？
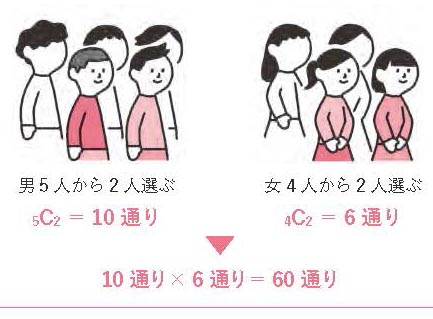
これには、まず男女それぞれから代表2人を選ぶ方法を考えます。男5人から代表2人を選ぶ方法は、5人から2人を選ぶ組み合わせなので
5Ｃ2＝（5×4）÷（2×1）＝10通り
女4人から代表2人を選ぶ方法は、4人から2人を選ぶ組み合わせなので
4Ｃ2＝（4×3）÷（2×1）＝6通り
男の代表1パターンに対し、女の代表は6パターン存在するので、男女2人ずつ代表を選ぶときの組み合わせは次のようになります。
10通り×6通り＝60通り
100 人から99人を選ぶ方法は
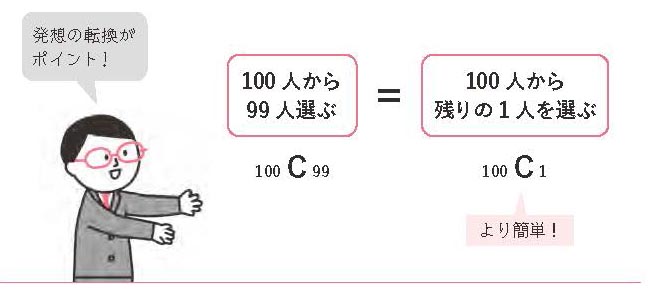
それでは100人から99人を選ぶときの組み合わせは、何通りあるでしょうか？
これは100Ｃ99の計算をしてもよいのですが、反対のことを考えると、もっと簡単に求めることができます。100人から99人を選ぶというのは、100人から残りの1人を選ぶことと同じなので、その1人の選び方を考えるのです。
100人から1人を選ぶ方法は100通りあります。したがってその反対、100人から99人を選ぶ組み合せも100通りということになります。
一般的に、次の公式が成り立つのです。
nＣr＝nＣn-r
よって、100人から99人を選ぶときの組み合わせをこの公式を使って表すと、以下になります。
100Ｃ99＝100Ｃ100-99＝100Ｃ1
出典：『マンガでわかる 図解 眠れなくなるほど面白い 確率の話』
【書誌情報】
『マンガでわかる 眠れなくなるほど面白い 図解 確率の話』
著者：野口哲典（マンガ：田伊りょうき）
当社の「眠れなくなるほど面白い 図解」シリーズをよりわかりやすく解説する「マンガ図解」シリーズの第１弾！ 我々の日常に深く入り込んでいる「確率」。朝の天気予報で「降水確率」を確認したり、野球シーズンには勝率や打率をチェックしたりする方もいると思います。ジャンケンやサイコロの目、ゲームのガチャやくじなどの当たる確率、人生の節目にあたる受験の合格確率やプロポーズの成功確率など、実にさまざまなシーンで「確率」の話になるのです。そんな「確率」をマンガと図で解説し、面白く読み進めながら知識を得られる一冊。「運命の出会い」を確率にするとどのくらいになるのか、最低でも一校は合格するための受験の仕方など、勉強としてではなく実際に役立つ確率の話ばかりなので、ぜひご一読ください。
公開日：2024.06.23
- この記事を共有する！
オススメ記事
