弧度法と度数法っていったい何？【眠れなくなるほど面白い 図解 大人のための算数と数学】
弧度法と度数法っていったい何？
円の一周を360度とする「度数法」は多くの人が知っていると思います。しかし「弧度法」はあまり聞き慣れない言葉ではないでしょうか。しかしこの「弧度法」を使うと角度に関する計算がシンプルになります。
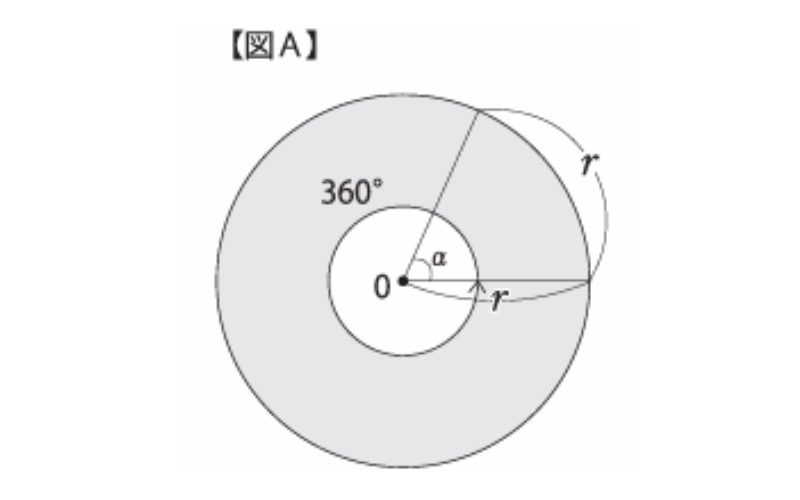
半径と同じ長さの弧に対する中心角をとり、これを単位とする角の表し方が「弧度法」です。【図A】において弧の長さは中心角に比例しますから、r:2πr＝α:360 α＝180°/πによりα＝57.29゜このαは「円の半径に関係しない一定の角」となります。半径の大きさにとらわれないということになり、応用範囲が広がるというのがポイントです。
このαを1ラジアン (1R) といいます。1R＝180°/πから180°＝πR、360°＝2πRとなります。
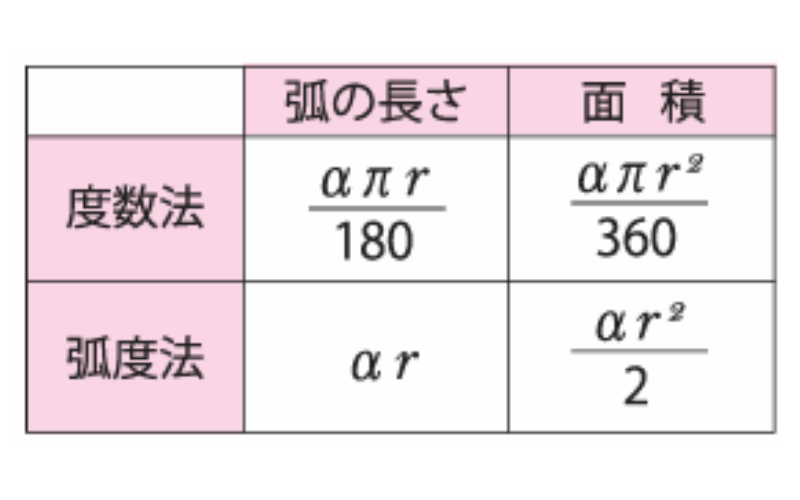
弧度法を使うメリットを度数法と比較して簡潔に示すと【図B】のようになります。（注）180°は弧度法ではπ（ラジアン）となる。
ここでは詳しい説明は割愛しますが、高校数学で登場する三角関数の極限などの計算は弧度法を使うと簡単に速くできることが予想できます。三角関数は物理などへの応用範囲が広まっています。
【図B】
半径r、中心角αの扇形の弧の長さと面積(180＝πとすると、弧度法の表示になる）
【出典】『眠れなくなるほど面白い 図解 大人のための算数と数学』監修：小宮山 博仁
【書誌情報】
『眠れなくなるほど面白い 図解 大人のための算数と数学』
監修：小宮山 博仁
算数や数学は、基本的な考え方さえわかれば、とても簡単で面白い!?
文系人間をはじめ苦手意識の強い小中高の算数と数学をまるごと、一気に学び直す一冊。
大人になった今だからこそら理解できる。
さらに実社会で、日常生活でどんなことに利用、活用、応用されているかを知ると、より身近に感じられ、その必要性がわかる。
本書を読めば、算数・数学が好きになり、「数学的な思考」を手に入れることができる!
この記事のCategory
オススメ記事
「できる」と「わかる」の境界線。算数と数学の違いとは？【眠れなくなるほど面白い 図解 大人のための算数と数学】
ホールインワンは雷に打たれる確率とほぼ同じ!? 日常生活に隠れている確率やデータ【眠れなくなるほど面白い 図解 大人のための算数と数学】
図形は身のまわりにあふれてる！算数が教える「カタチの意味」【眠れなくなるほど面白い 図解 大人のための算数と数学】
「やぎ算」で論理力が爆上がり!? ビジネスにも使える算数の考え方とは【眠れなくなるほど面白い 図解 大人のための算数と数学】
［生活の中にある確率］じゃんけんで勝つ確率はどれくらい？【眠れなくなるほど面白い 図解 大人のための算数と数学】
数学がもっと面白くなる！「＋｣や｢－」が生まれた起源とは？【眠れなくなるほど面白い 図解 大人のための算数と数学】
数字に“単位”をつけるだけで、世界がわかりやすくなる話【眠れなくなるほど面白い 図解 大人のための算数と数学】
神社に数学の問題を奉納!? 知られざる「算額文化」とは【眠れなくなるほど面白い 図解 大人のための算数と数学】
