円周率3.14の謎を解明? 円の面積公式の真実とは【眠れなくなるほど面白い 図解 大人のための算数と数学】


円の面積はなぜ半径×半径×3.14で求められるの?
円をおうぎ形に分解してその面積を求めてみる
【図A】は中心0とする直径10cmの円です。円周を調べようと思ったら、細いひもを周囲に這(は)わせて計ることは小学生でも可能です。
だいたい31cmの長さになります。直径の約3.1倍で、どんな大きさの円も同じになり、これを円周率といいます。円周率を詳しく調べると、3.14159…と続く、循環しない無限小数(無理数)であることがわかっています(この円周率のことを数学ではπで表します)。円の面積を求める公式は小学校高学年で学びます。半径をrとすると、円の面積Sは、r×r×3.14で求められます。
S=r×r×3.14またはS=πr²となります。
【図A】では、5×5×3.14=78. 5で面積は78.5cm²です。
大人なら、ほとんどの人は暗記している公式ではないでしょうか。しかし、どうして「半径×半径× 3.14」で円の面積を求めることができるのか、それを説明するのはかなり大変です。本格的に理解しようと思ったら「微分積分」を活用することになるからです。
ここでは円を等分していく方法を紹介しましょう。
【図B】の①から③のように8等分、16等分、32等分としていくと④のような長方形に近づいていきます。最初の①の円と④の長方形ABCDの面積は同じになります。
ABは半径で5cmです。BC+ADは円周(10×3.14=31.4cm)です。BCは31.4の半分の15.7となります。これは(10×3.14)÷2=5×3.14=15.7 と考えることができます。5は半径です。これをrとすると、 AB×BC=r×r×3.14=3.14r²となります (AB=r、BC=r×3.14)。

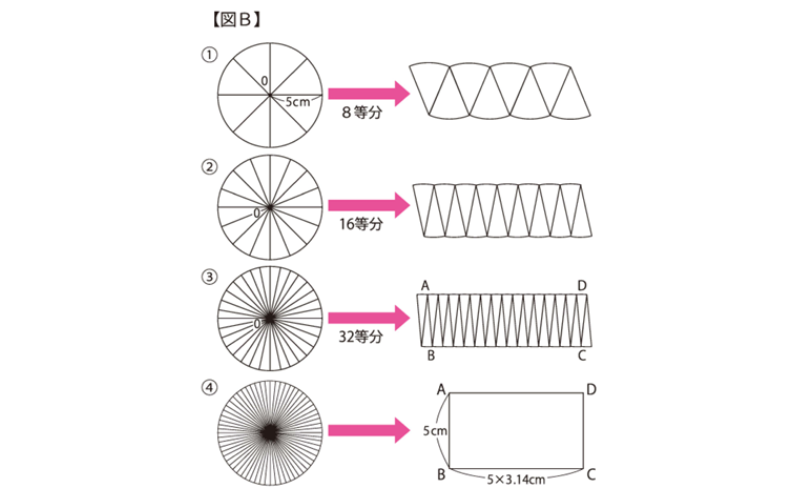
円を8等分、16等分、32等分…と細かく分けていくと、最終的にはタテが半径、ヨコが半径×3.14倍の長方形に近づいていきます!
【POINT】
円なのに長方形にして面積を考える発想が大切です。円の面積の公式だけを暗記するのではなく、公式を求める過程を理解することによって、柔軟な考えが身につきます。
【出典】『眠れなくなるほど面白い 図解 大人のための算数と数学』監修:小宮山 博仁
【書誌情報】
『眠れなくなるほど面白い 図解 大人のための算数と数学』
監修:小宮山 博仁
算数や数学は、基本的な考え方さえわかれば、とても簡単で面白い!?
文系人間をはじめ苦手意識の強い小中高の算数と数学をまるごと、一気に学び直す一冊。
大人になった今だからこそら理解できる。
さらに実社会で、日常生活でどんなことに利用、活用、応用されているかを知ると、より身近に感じられ、その必要性がわかる。
本書を読めば、算数・数学が好きになり、「数学的な思考」を手に入れることができる!
この記事のCategory
オススメ記事

「できる」と「わかる」の境界線。算数と数学の違いとは?【眠れなくなるほど面白い 図解 大人のための算数と数学】

1メートル=地球の1000万分の1!? 意外と知らないメートル法の起源【眠れなくなるほど面白い 図解 大人のための算数と数学】

100%儲かるはずが…現実は? マーチンゲール法の落とし穴【眠れなくなるほど面白い 図解 大人のための算数と数学】

「ねずみ講」はなぜ違法? マルチ商法の違いとは【眠れなくなるほど面白い 図解 大人のための算数と数学】

ホールインワンは雷に打たれる確率とほぼ同じ!? 日常生活に隠れている確率やデータ【眠れなくなるほど面白い 図解 大人のための算数と数学】

世界中で使われる「美しい比率」黄金比vs白銀比! 好きなのはどっち?【眠れなくなるほど面白い 図解 大人のための算数と数学】

弧度法と度数法っていったい何?【眠れなくなるほど面白い 図解 大人のための算数と数学】

数字に“単位”をつけるだけで、世界がわかりやすくなる話【眠れなくなるほど面白い 図解 大人のための算数と数学】
求人情報
「auショップスタッフ」/未経験OK/残業月3時間/20代30代活躍中/面接1回のみ/個人ノルマなし
auショップ みなみ野駅前店
勤務地:東京都雇用形態:正社員給与:月給22万円~26万円スポンサー:求人ボックス
工具や設備の製作や部品加工 新型自動車開発関連 完全週休2日制 資格取得支援制度 未経験可 車通勤可
株式会社タイコー
勤務地:愛知県雇用形態:正社員給与:年収350万円~500万円スポンサー:求人ボックス
小中学校の調理師
株式会社レクトン
勤務地:東京都雇用形態:正社員給与:月給21万円~25万円スポンサー:求人ボックス
冠婚葬祭プランアドバイザー
株式会社117
勤務地:大阪府雇用形態:正社員給与:月給20万円~スポンサー:求人ボックス
住宅型有料老人ホームの夜勤専従スタッフ
株式会社川商
勤務地:大阪府雇用形態:アルバイト・パート給与:日給2万2,000円スポンサー:求人ボックス
廃棄物収集ドライバー
株式会社JR東日本環境アクセス
勤務地:東京都雇用形態:契約社員給与:月給25万円~34万2,000円スポンサー:求人ボックス




